[無料ダウンロード! √] 場合の数 組み合わせ方 237218-場合の数 組み合わせ方
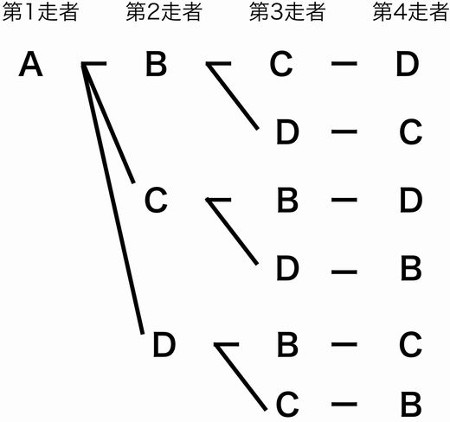
ならない取り出し方の場合は組合せで考えればいいわけです。 では、問題を考えてみましょう。 1 (1)は「第1走者から第4走者までの4人を選ぶ・・・」 つまり、順序が問題になるので、『順列』の考えで。 4は「男子6人、女子10人の中から男子3人、女子4人
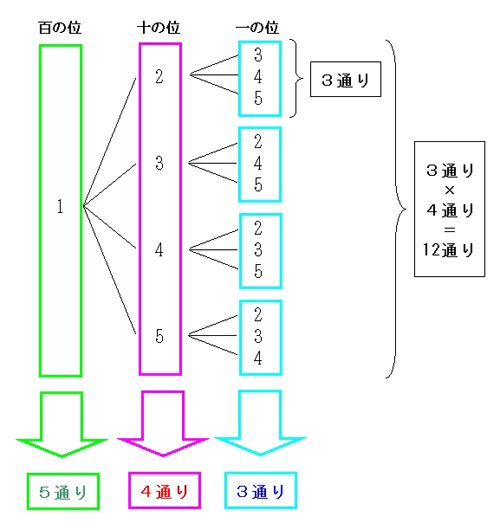
場合の数 組み合わせ方-計算例 ドからシまでの12個の半音から7つの音を選んだ場合何通り作れるか 導入の検討をしている顔認識ツールに対する性能評価のため。 nC2としたとき十分な組み合わせの数が得られるものを適当に確認した事柄Aの起こり方がm通りあり,その各々に対して事柄Bの起こり方がn通りあるとき,AとBがともに起こる場合の数は( m×n )通りである。 もう少し簡単な考え方としては,
場合の数 組み合わせ方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
 |  |  |
「場合の数 組み合わせ方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「場合の数 組み合わせ方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「場合の数 組み合わせ方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
 |  |  |
「場合の数 組み合わせ方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
 |  |  |
「場合の数 組み合わせ方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「場合の数 組み合わせ方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「場合の数 組み合わせ方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  | |
「場合の数 組み合わせ方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |
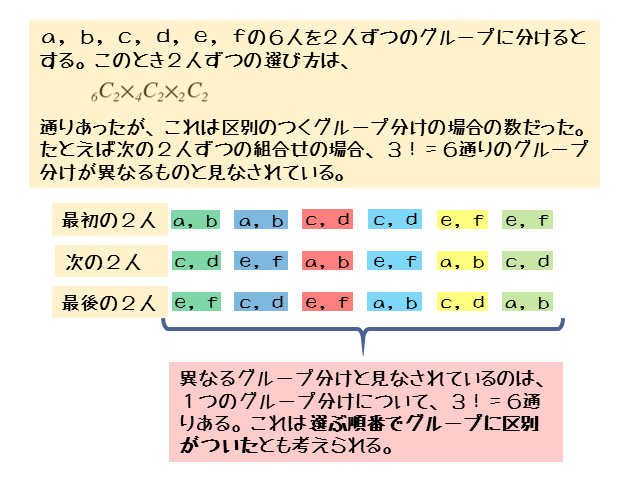
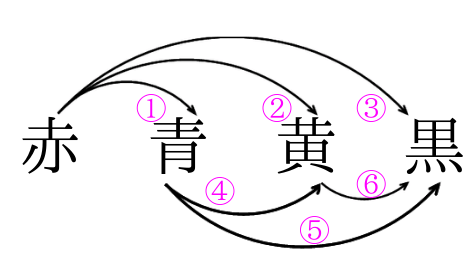
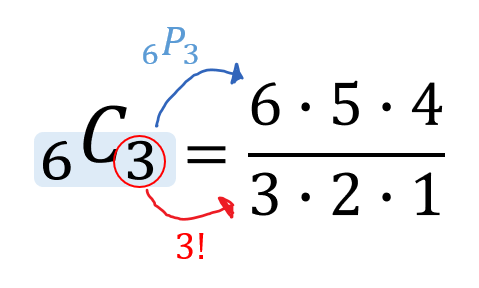
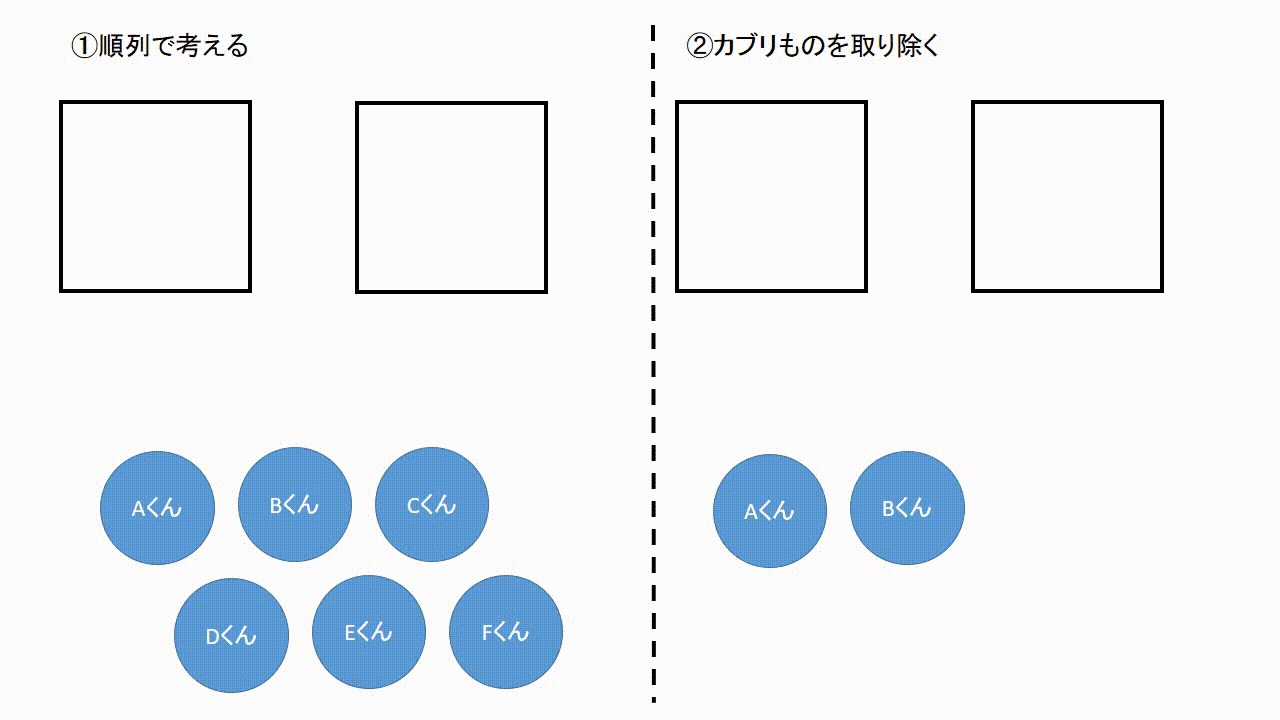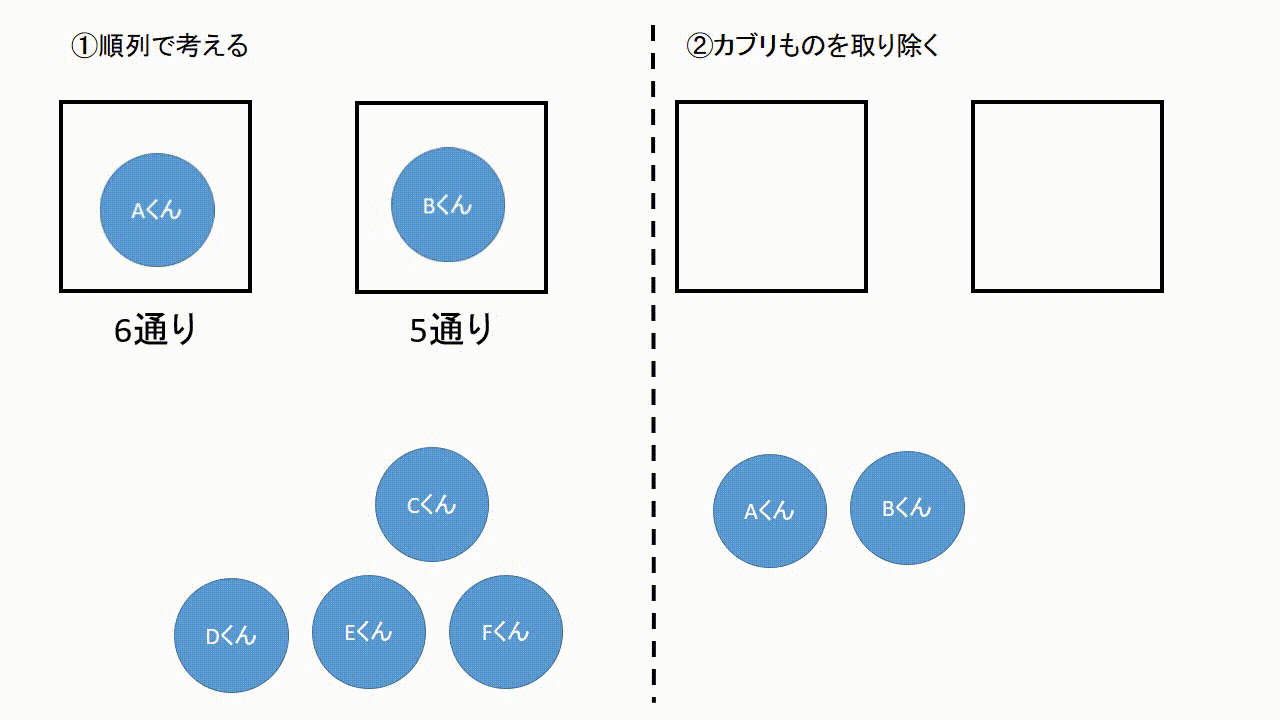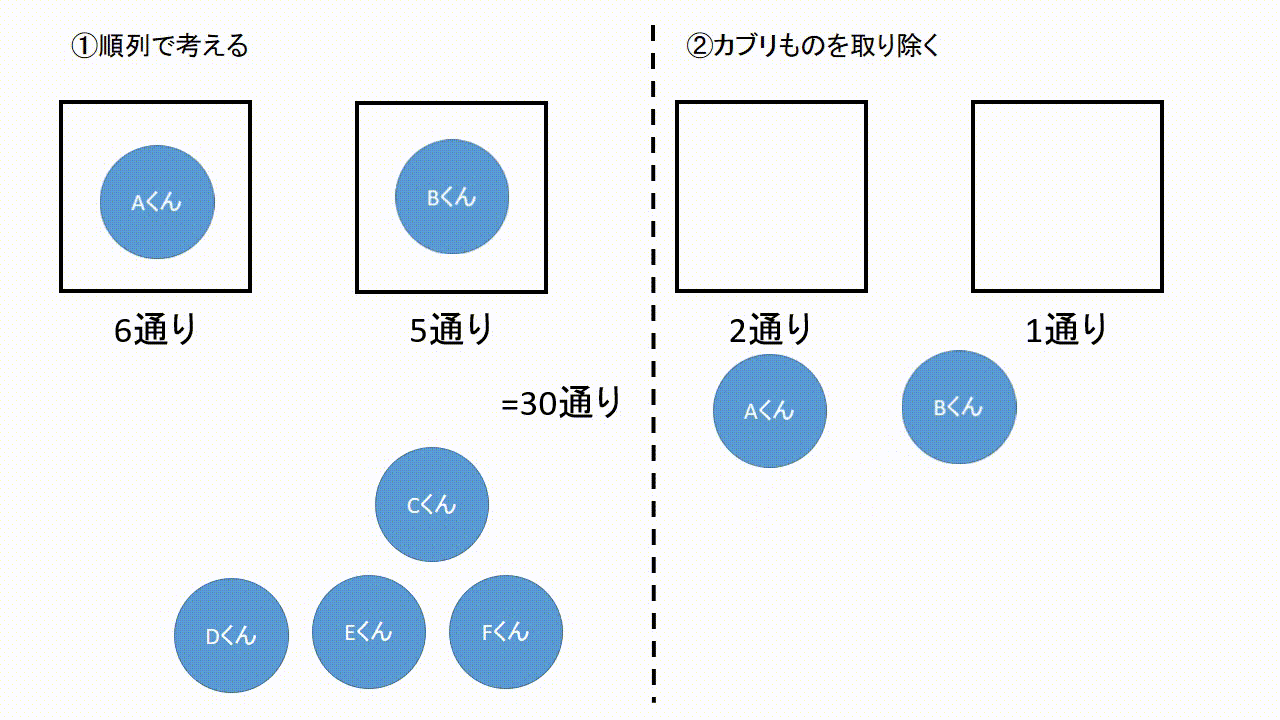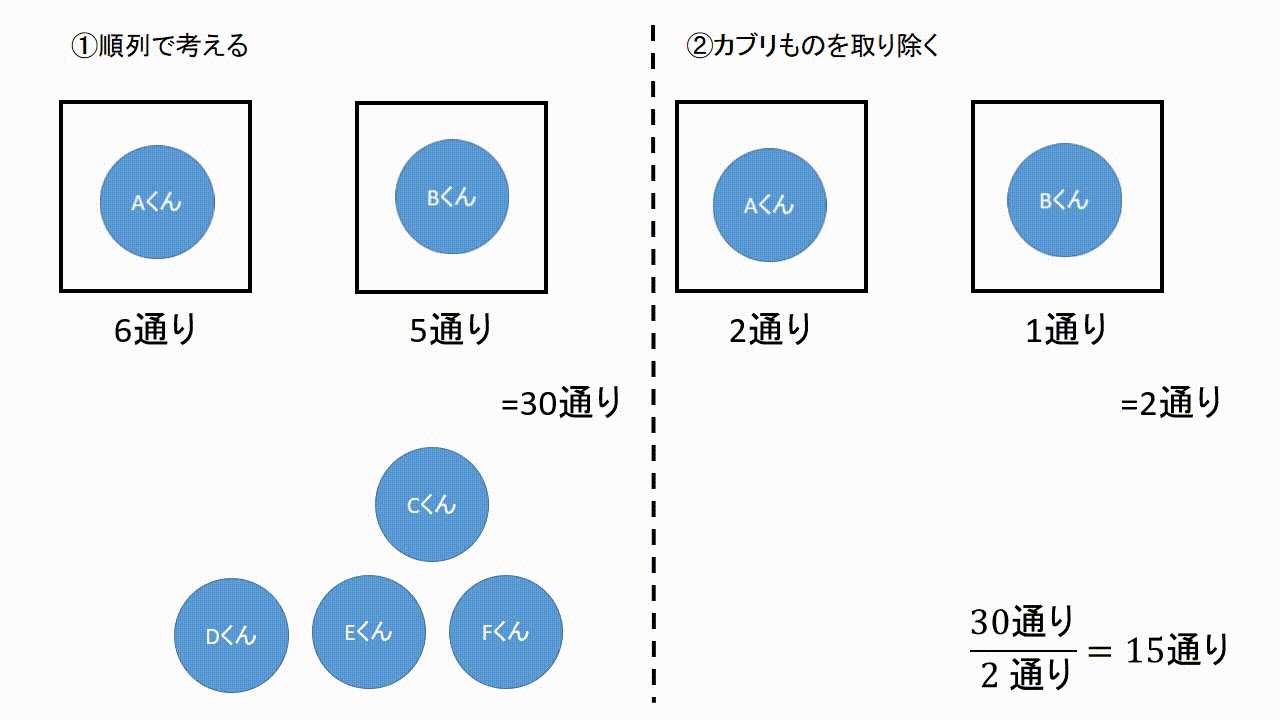
この2種類の問題では、それぞれ答えが変わってきます。 ①は順列で、答えは 5 p 2 =5×4=通り ②は組み合わせで、答えは 5 c 2 =5×4÷2=10通りになります。 今回は、そんな順列と組み合わせの数の考え方についてです。 (2) 組み合わせの考え方 組み合わせが順列と異なる点は、 選んだ順番を考慮しない ところでしたね。 具体歴な例で「選んだ順番を考慮しない」ことが組み合わせの数にどう影響するかを見ていきましょう。
Incoming Term: 場合の数 組み合わせ方,
コメント
コメントを投稿