√ダウンロード 対角線の長さが等しい四角形 面積 111191

ボード 勉強 のピン

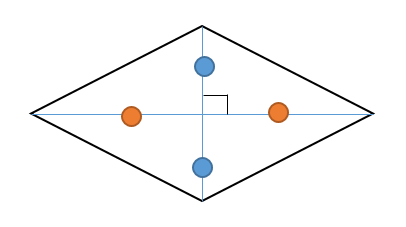
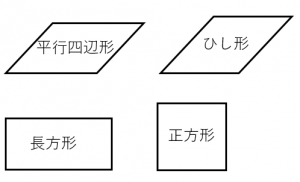
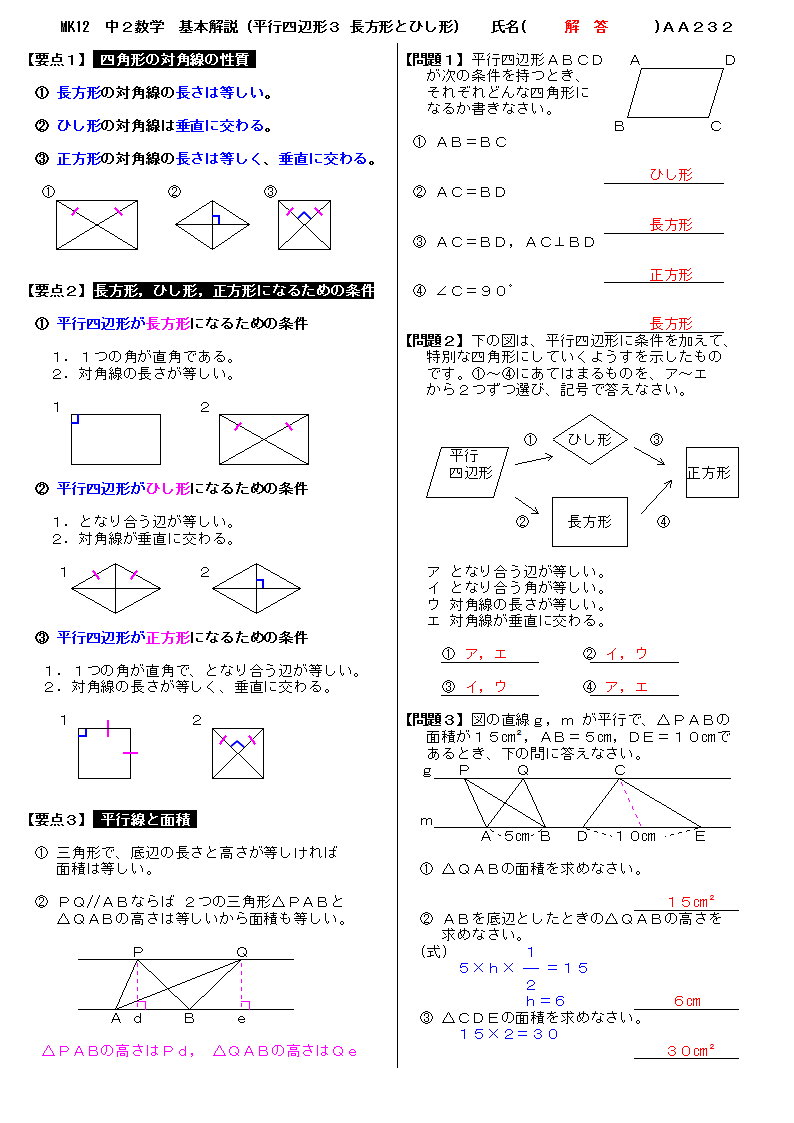
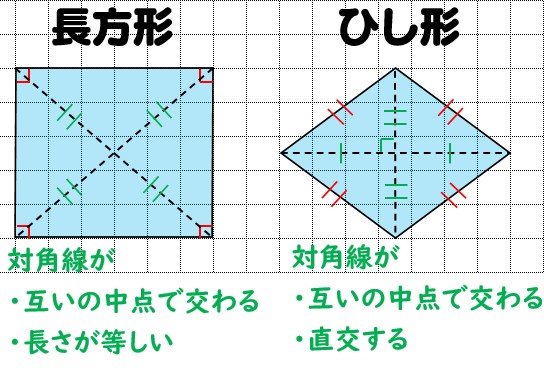
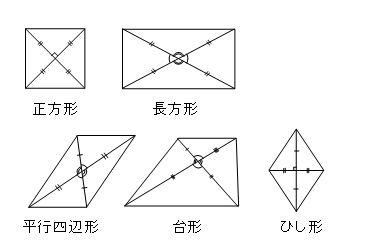
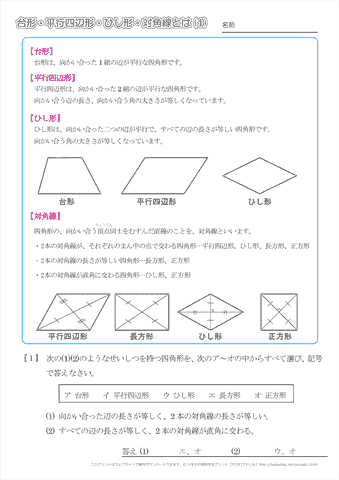
 平行四辺形の対角線の条件に、「 2本の対角線の長さが等しい 」 「 2本の対角線が垂直 ( 90° ) に交わる 」 と言う2つの条件が加われば、正方形になります。 正方形、長方形、ひし形はいずれも平行四辺形であり、平行四辺形の中でも、一定の条件を追加し②斜辺と他の1辺がそれぞれ等しい 8 二等辺三角形の性質 ①両底角が等しい ②頂点の二等分線と底角の垂直二等 分線は一致する 9 平行四辺形の性質 ①2組の向かい合う辺はそれぞれ等しい ②1組の向かい合う辺が平行で等しい ③2組の向かい合う角は

対角線の長さが等しい四角形 面積

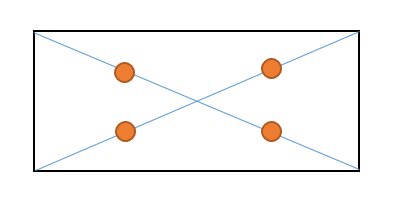
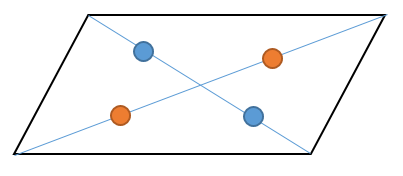
対角線の長さが等しい四角形 面積-・平行四辺形には、下のような3つの性質があります。 1．対辺の長さが等しい 2．対角の角度が等しい 3．対角線は中点で交わる 今回、3つ目の平行四辺形の性質である、 対角線は中点で交わる ことを確認していきたいと思います。この2つの性質を利用して考えていきます。 すると ということがわかります。 グラフ上で、それぞれの辺が平行で長さが等しいということは このように、 それぞれの移動距離が等しくなる ということを表しています。 AからOまでは、横に3と下に2移動

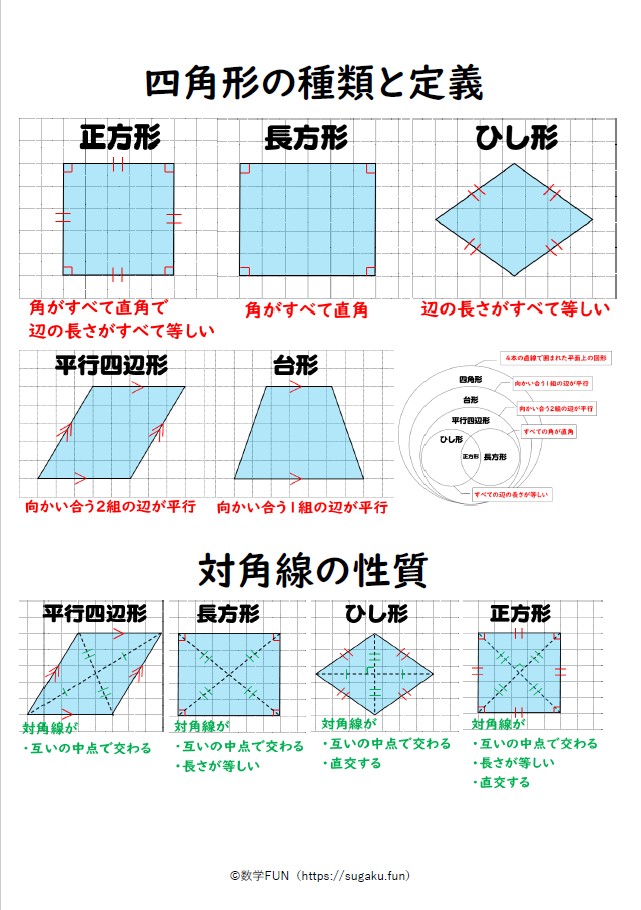
四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun

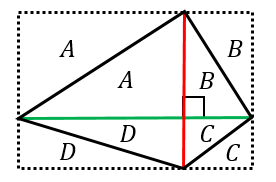
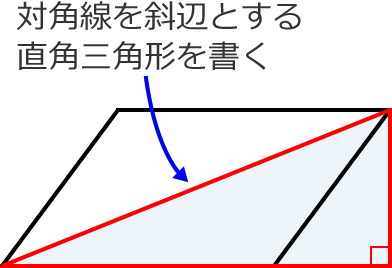
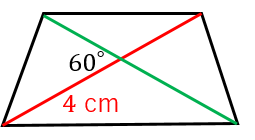
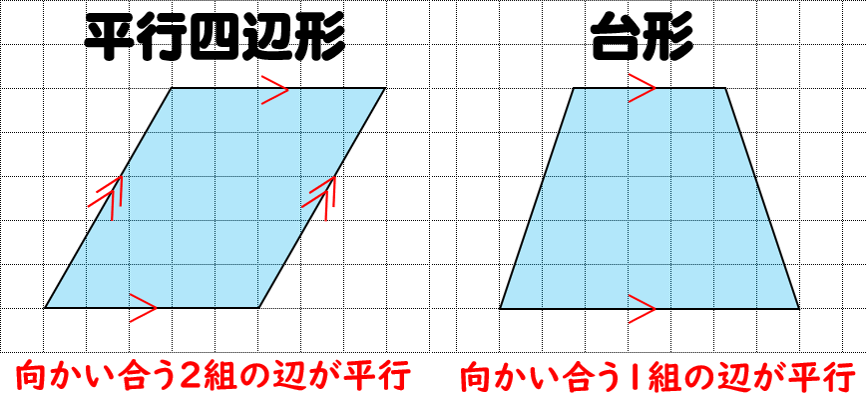
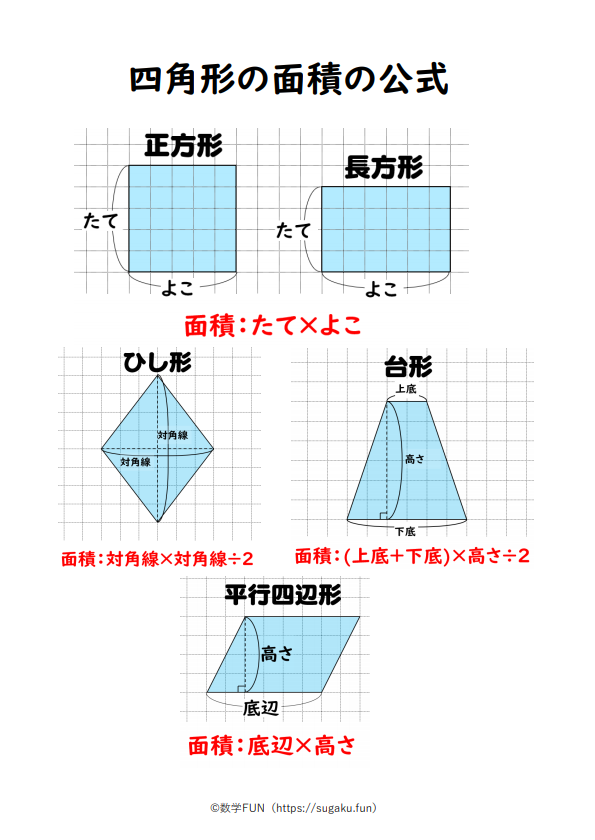
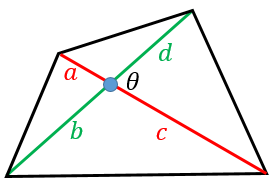
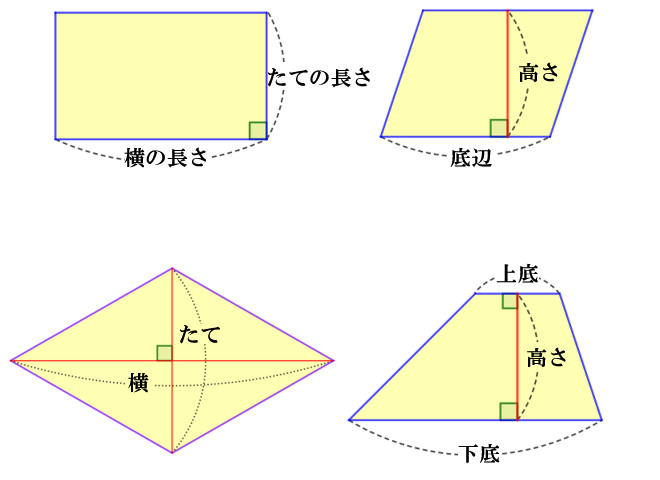
 平方四辺形を対角線で分けた $4$ つの三角形の面積は等しいから、平行四辺形の面積は、 $4\times \dfrac{3\sqrt{3}}{2} = 6\sqrt{3}$ だね！ まとめ 平行四辺形の面積を対角線の長さと角度から求めるのに必要な特徴は、 底辺比2：3が2つの三角形の面積比になる。三角形adeが9なので三角形abeは6と分かる。 三角形の面積比は求められました。最後に右側の四角形部分です。 5合同な三角形から四角形の面積比 平行四辺形の左上と右下で、2つの三角形にわけてみます。対角線を・ 平行四辺形の面積＝底辺×高さ ・ 台形の面積＝（上底＋下底）×高さ÷2 ・ ひし形の面積＝対角線×対角線÷2 面積の公式 ⑴ 三角形 ⑵ 平行四辺形 高さが三角形や平行四辺形の外にある図形でも，公式をつかって，図形の面

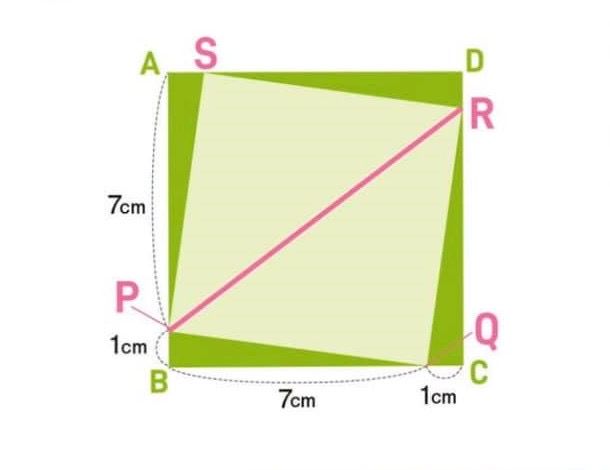
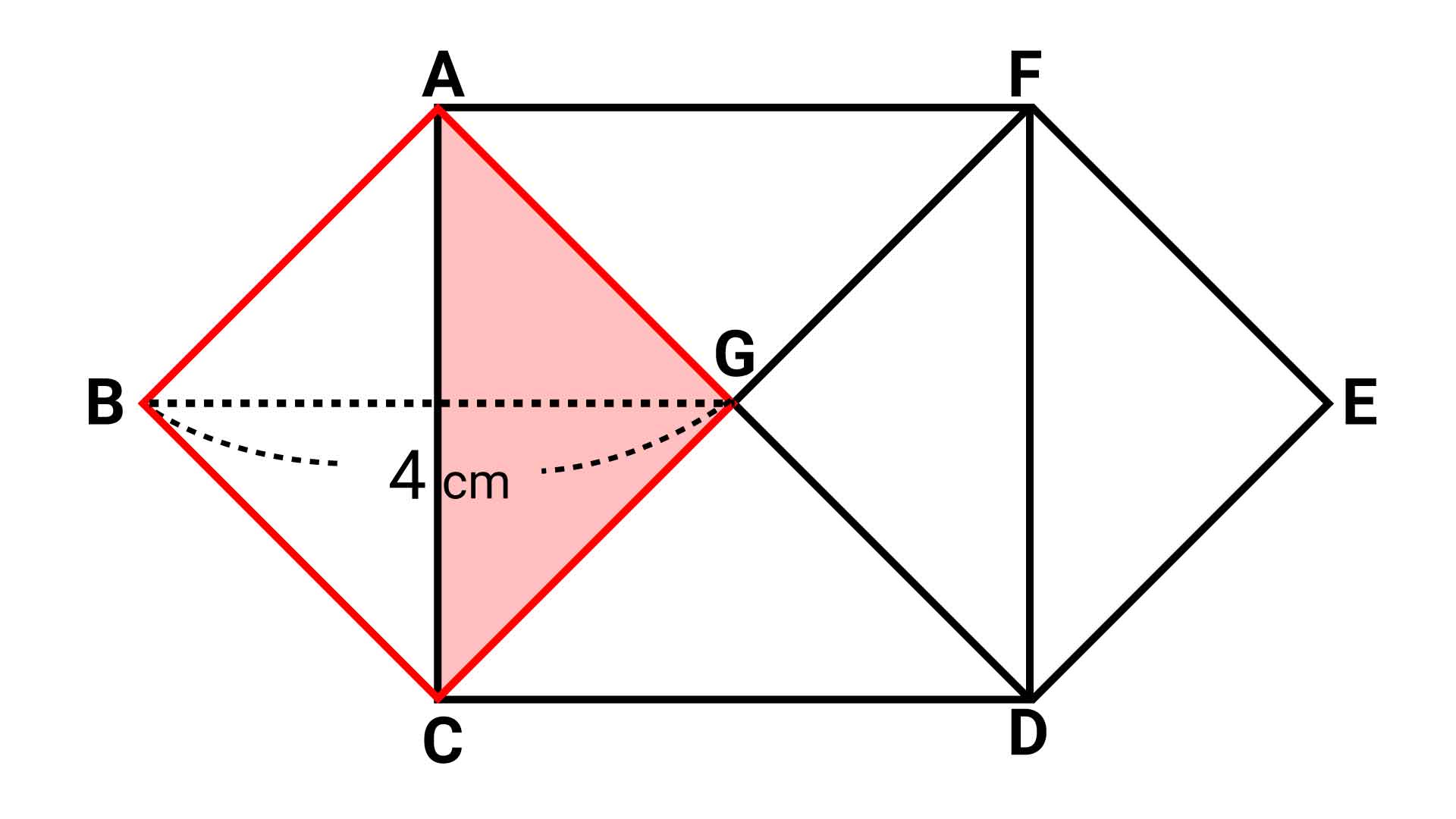
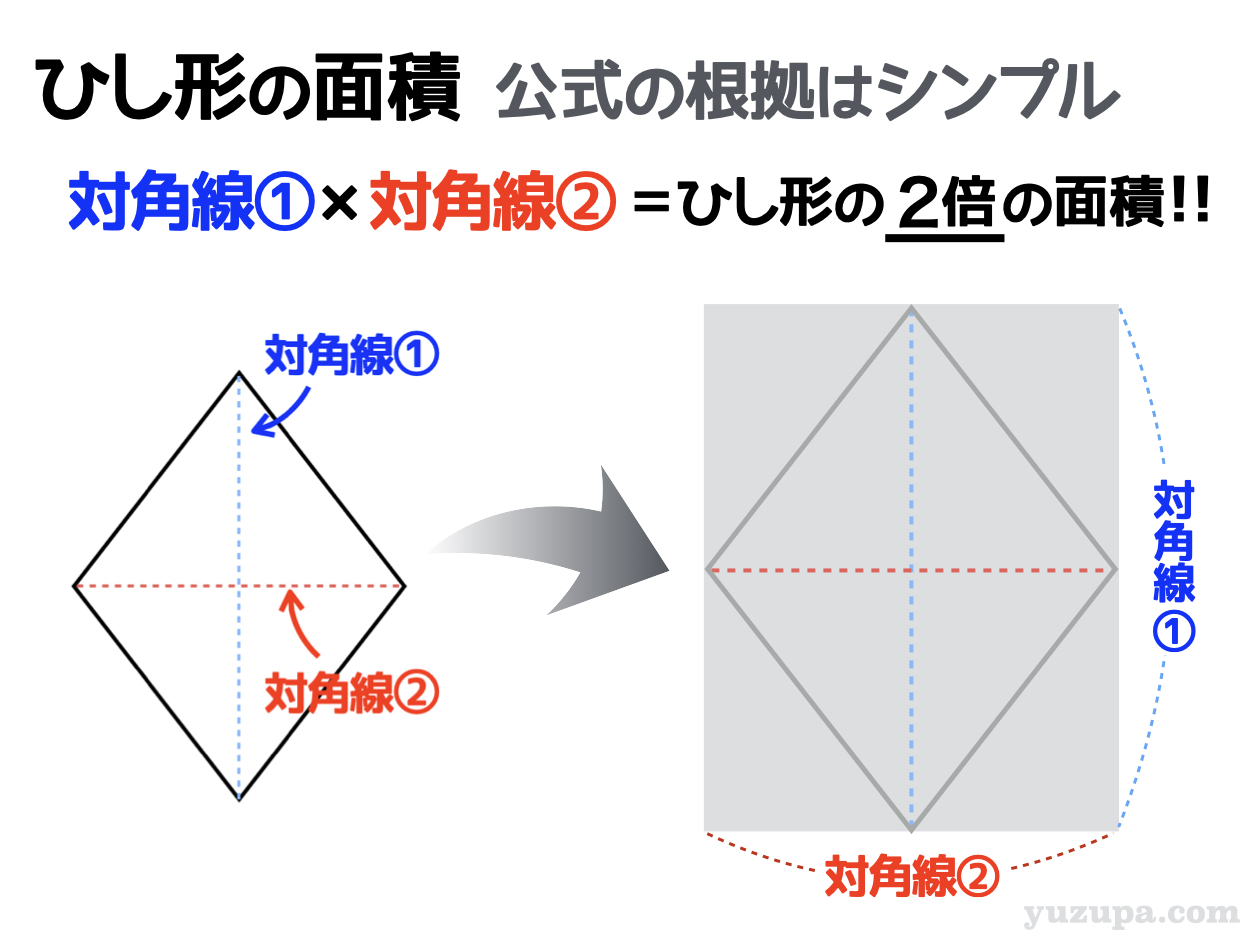
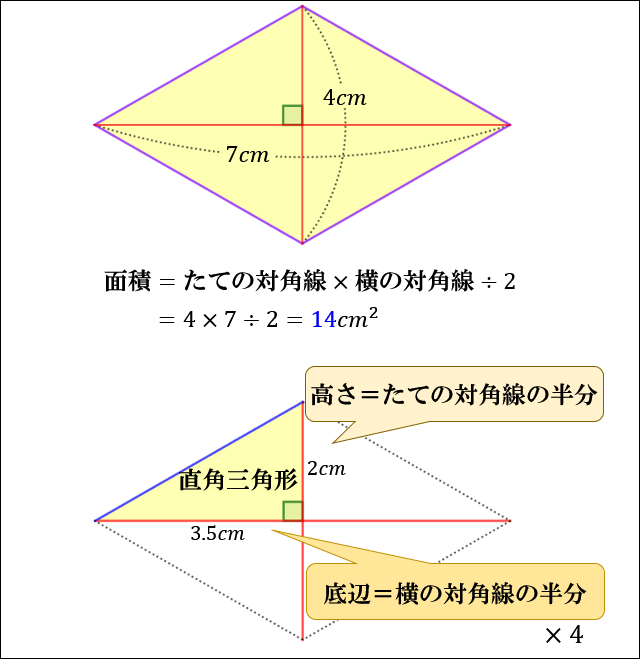
 正多角形の対角線の長さ 本記事では、一辺の長さがaである正多角形 (正 n 角形、nは 4 以上の整数)の対角線の長さについて考えます。 対角線の長さは一般に複数種類あるので、その全てを紹介します。 なお、正三角形は対角線を持たないので除外します。 ひし形を囲った長方形のたてと横の長さは、ひし形の直角に交わる対角線の長さと等しいので、対角線×対角線÷2 = 4×3÷2 = 6㎠ となります。 ④台形の面積 次に上底1cm、下底3cm、高さ3cmの台形の面積を求めます。 1 bdに対角線を引く。 2 aを通るbdに平行な直線を引く。 3 cbと延長して、bdと交わった所をeと置く すると、三角形abdと三角形ebdが同じ面積となり(底辺は同じで、高さが等しいから)、三角形bdcは共有しているので、

対角線の長さが等しい四角形 面積のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「対角線の長さが等しい四角形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「対角線の長さが等しい四角形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「対角線の長さが等しい四角形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「対角線の長さが等しい四角形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「対角線の長さが等しい四角形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「対角線の長さが等しい四角形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「対角線の長さが等しい四角形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「対角線の長さが等しい四角形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「対角線の長さが等しい四角形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「対角線の長さが等しい四角形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「対角線の長さが等しい四角形 面積」の画像ギャラリー、詳細は各画像をクリックしてください。

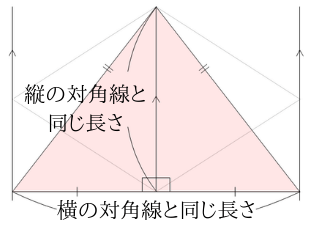
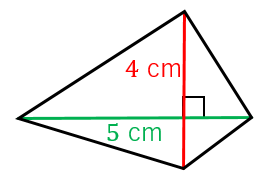
 正多角形をすべての対角線で分けた二等辺三角形の面積を求めて、その和を求める方法もあるので、上記の公式を無理して覚える必要はありません。 （二等辺三角形に分ける方法については、計算問題①で解説します！） 正 n 角形の面積の公式（n = 3, 4, 5, 6）例： 対角線の長さが19mと5mのたこ形があるとします。これの面積は、(19 × 5)/2 = 95/2 = 475 ㎡です。 対角線の長さが分からず、測ることもできない場合、三角関数を用いて求めることができます。詳しくは以下を見ていきましょう。